
公式
1反向行程问题公式
反向行程问题可以分为“相遇问题”和“相离问题”两种。
这两种题,都可用下面的公式解答:
×相遇时间=相遇路程;
相遇路程÷=相遇时间;
相遇路程÷相遇时间=速度和。
2相遇问题公式
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
3工程问题公式
一般公式:
工效×工时=工作总量;
工作总量÷工时=工效;
工作总量÷工效=工时。
用假设工作总量为“1”的办法解工程问题的公式:
1÷工作时间=单位时间内完成工作总量的几分之几;
1÷单位时间能完成的几分之几=工作时间。
4收益与打折公式
收益=售出价-本钱
利率=收益÷本钱×100%=×100%
涨跌金额=本金×涨跌百分比
打折=实质价格÷原价格×100%
利息=本金×利率×时间
税后利息=本金×利率×时间×
5浅易方程要点
1、用字母表运算定律。
加法交换律:a+b=b+a 加法结合律:a+b+c=a+
乘法交换律:a×b=b×a 乘法结合律:a×b×c=a×
乘法分配律:×c=a×c±b×c
2、用字母表示计算公式。
长方形的周长公式:c=×2 长方形的面积公式:s=ab
正方形的周长公式:c=4a 正方形的面积公式:s=a×a
3、 读作:x的平方,表示:两个x相乘。
2x表示:两个x相加,或者是2乘x。
4、①含有未知数的等式称为方程。
②使方程左右两边相等的未知数的值叫做方程的解。
③求方程的解的过程叫做解方程。
5、把下面的数目关系补充完整。
路程=× 速度=÷ 时间=÷
总价=× 单价=÷ 数目=÷
总产量=× 单产量=÷
数目=÷
工作总量=×
工作效率=÷
工作时间=÷
大数-小数=相差数 大数-相差数=小数 小数+相差数=大数
一倍量×倍数=几倍量 几倍量÷倍数=一倍量
几倍量÷一倍量=倍数
被减数=减数+差 减数=被减数-差 加数=和-另一个加数
被除数=除数×商 除数=被除数÷商 因数=积÷另一个因数

考试试题
1. 解下列方程:
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ;(4)
;(4)![]() ;
;
(5)![]() ; (6)
; (6)![]() ÷0.4=2.2。
÷0.4=2.2。
考查目的:考查学生依据等式的性质解方程的能力。
答案:
(1)![]() ;(2)
;(2)![]() ;
;
(3)![]() ;(4)
;(4)![]() ;
;
(5)![]() ;(6)
;(6)![]() 。
。
分析:
依据“两边同时加上或减去同一个数,等式仍然成立”“等式两边同时乘或除以同一个数,等式仍然成立”即可解方程。
(1)第一依据等式的性质,两边同时减去12,然后两边再同时除以4即可;
(2)第一化简,然后依据等式的性质,两边同时除以3即可;
(3)第一化简,然后依据等式的性质,两边同时除以7即可;
(4)依据等式的性质,两边同时加上4,然后再两边同时除以6即可;
(5)依据等式的性质,两边同时加上120即可;
(6)依据等式的性质,两边同时乘以0.4即可。
2.如图:

求故事书的数目。
考查目的:考查学生理解、剖析等量关系,并依据等量关系列方程解决问题的能力。
答案:![]() =36。
=36。
答:故事书有36本。
分析:依据线段图剖析本题的等量关系:故事书的本数+文静书的本数=180,文静书的本数是故事书本数的4倍,据此可列方程进行解答。
解:设故事书有![]() 本,则文静书有
本,则文静书有![]() 本。
本。
![]() ,
,
![]() ,
,
![]() =36
=36
答:故事书有36本。
3.如图:
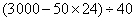
求![]() 的长度。
的长度。
考查目的:考查学生理解、剖析等量关系,并依据等量关系列方程解决问题的能力。
答案:![]() (米)。
(米)。
分析:依据线段图,![]() 加上22.5等于
加上22.5等于![]() ,由此列方程为
,由此列方程为![]() 。
。
解:![]() ,
,
![]() ,
,
![]() ,
,
![]() 。
。
4.实验小学图书馆新买来绘本和文学书共1000本,买来的文学书比绘本数目的2倍少50本。两种书各买了多少本?
考查目的:考查学生理解、剖析等量关系,并依据等量关系列方程解决问题的能力。
答案:绘本350本,文学书650本。 答:买来的绘本是350本,文学书是650本。
分析:依据题意,可得“绘本的数目+文学书的数目=1000”。
解:设绘本为![]() 本,则文学书为(2
本,则文学书为(2![]() -50)本。
-50)本。
![]() ,
,
![]() ,
,
![]() ,
,
![]() 。
。
![]() (本)。
(本)。
答:买来的绘本是350本,文学书是650本。
5.商店运来24筐梨和40筐苹果,一共重3000千克,每筐梨重50千克,每筐苹果重多少千克?(用两种办法解答)
考查目的:本题主要考查学生运用不同办法解决问题的能力。
答案: 45千克。
答:每筐苹果重45千克。
分析: 办法1、设每筐苹果重![]() 千克。
千克。
![]() ,
,
![]() ,
,
![]() ,
,
![]() 。
。
办法2、先求梨的重量,再求苹果的重量,最后依据“每筐苹果重量=苹果总重量÷筐数”列式求解。
![]()
![]()
![]()
![]() (千克)
(千克)
答:每筐苹果重45千克
声明:文章源自互联网,侵删








